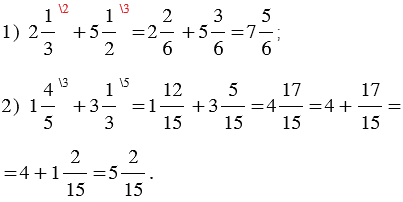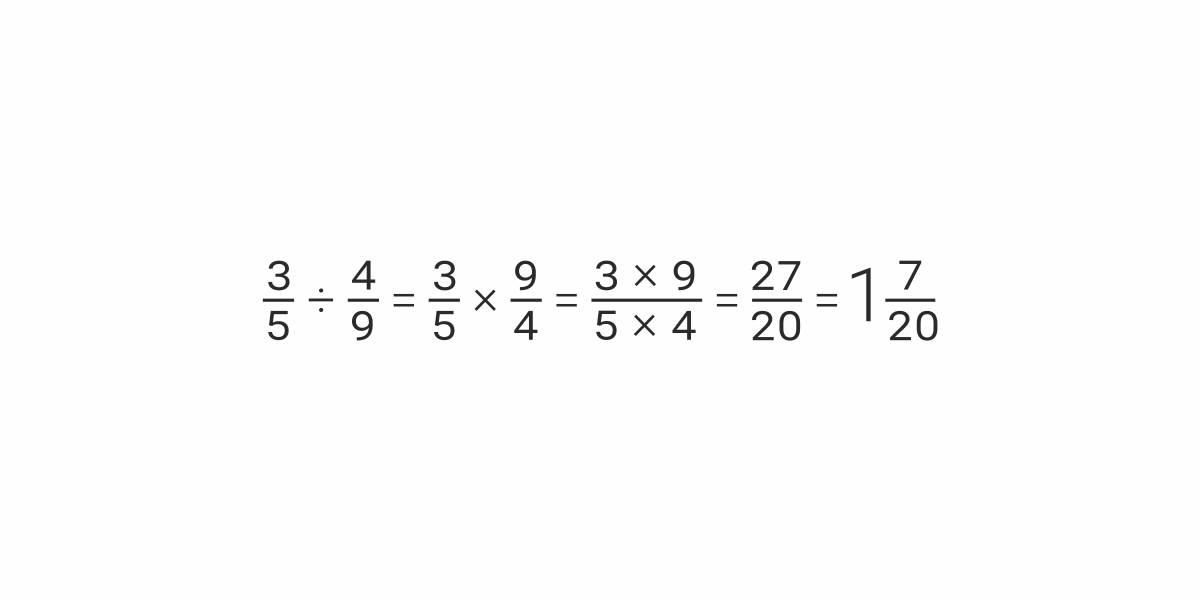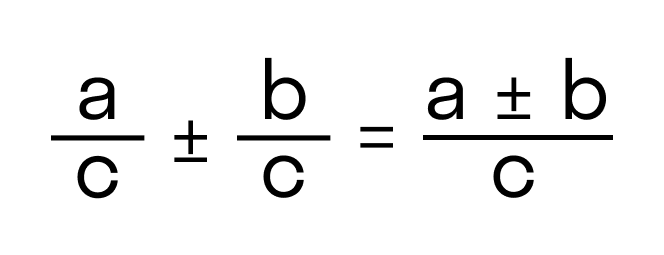
Вычитание дробей
Как научиться легко и быстро умножать дроби, можно ли научиться делать это в уме и как успешно подготовиться к контрольной — разбираем тему из школьной программы по математике вместе с экспертом. Как высчитать, чему равно произведение пяти восьмых и трех девятых? Или как умножить семь тринадцатых на четыре? Школьники России учатся этому, проходя одну из основных тем программы по математике — умножение дробей. Разберемся, для чего пригодится это умение, и узнаем у эксперта, как успешно подготовиться к контрольной.







Действия с дробями начинают учить в 6 классе. На первых уроках этой темы дети учатся добавлять и вычитать дроби с общим знаменателем. Позже переходят к умножению и делению. В будущих классах этот навык необходим для решения более сложных уравнений и задач по алгебре и геометрии. Mathema подготовила статью, которая быстро научит, как добавлять, вычитать, делить и умножать дроби. О том, как родители могут объяснить ребенку дроби, мы писали в одной из наших статей за ссылку.










Приведение дробей к общему знаменателю.
Суммой двух дробей с одинаковыми знаменателями называется дробь, числитель которой равен сумме числителей исходных дробей, а знаменатель - знаменателю дробей, то есть. Чтобы сложить две дроби с одинаковым знаменателем, надо сложить их числители и результат записать в числитель, а знаменатель оставить без изменения. Если в результате сложения получается дробь, числитель и знаменатель которой можно сократить, то для конечного результата выполняем и сокращение дроби. Складываются дроби с одинаковым знаменателем, поэтому просто складываем числитель, а знаменатель оставляем исходный:. Чтобы сложить дроби с разными знаменателями , вначале надо привести их к общему знаменателю, а далее складывать как дроби с общим знаменателем.